Optimising Forecasting Models for Diverse Time Series Data: A Case Study Approach

This task was undertaken as part of the Forecasting module during the first year of the Graduate Diploma program in Computer and Information Science. The implementation was carried out using the R programming language, with the objective of exploring various models across different datasets to identify the most accurate and effective model for each. The project utilised three distinct datasets to analyse and forecast time series data. The first case study focuses on monthly drug sales (HO3 anti-inflammatory drugs) in Australia from July 1991 to June 2008. The second and third case studies explore datasets from the global economy, focusing on New Zealand's economic trends and Australia's livestock data (pigs slaughtered in Victoria).

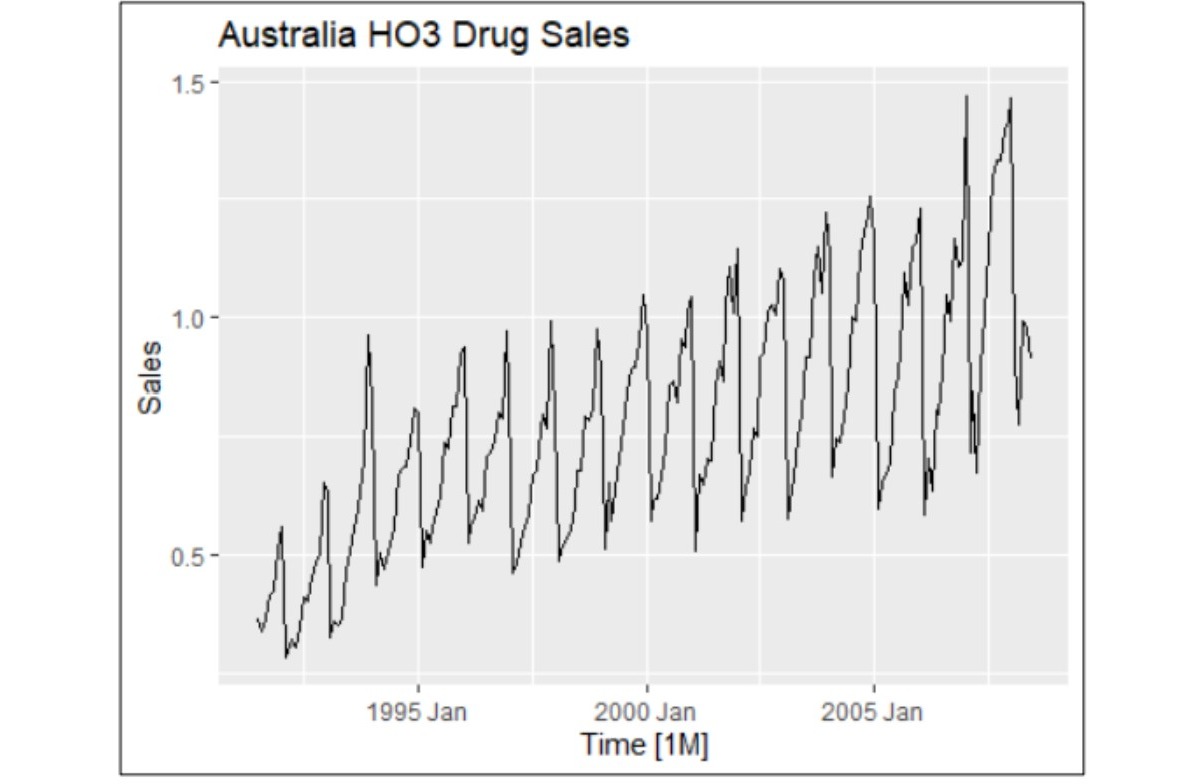
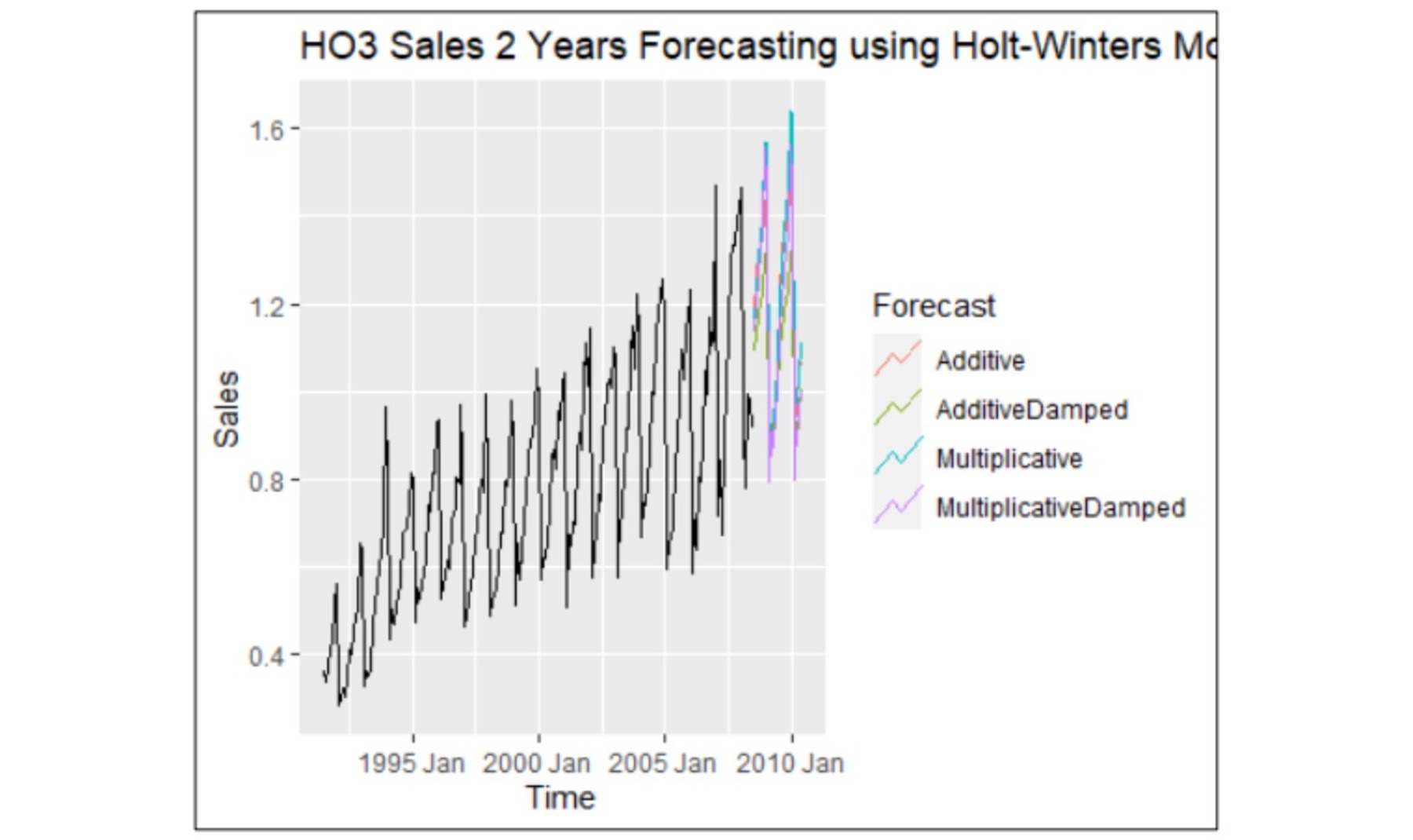
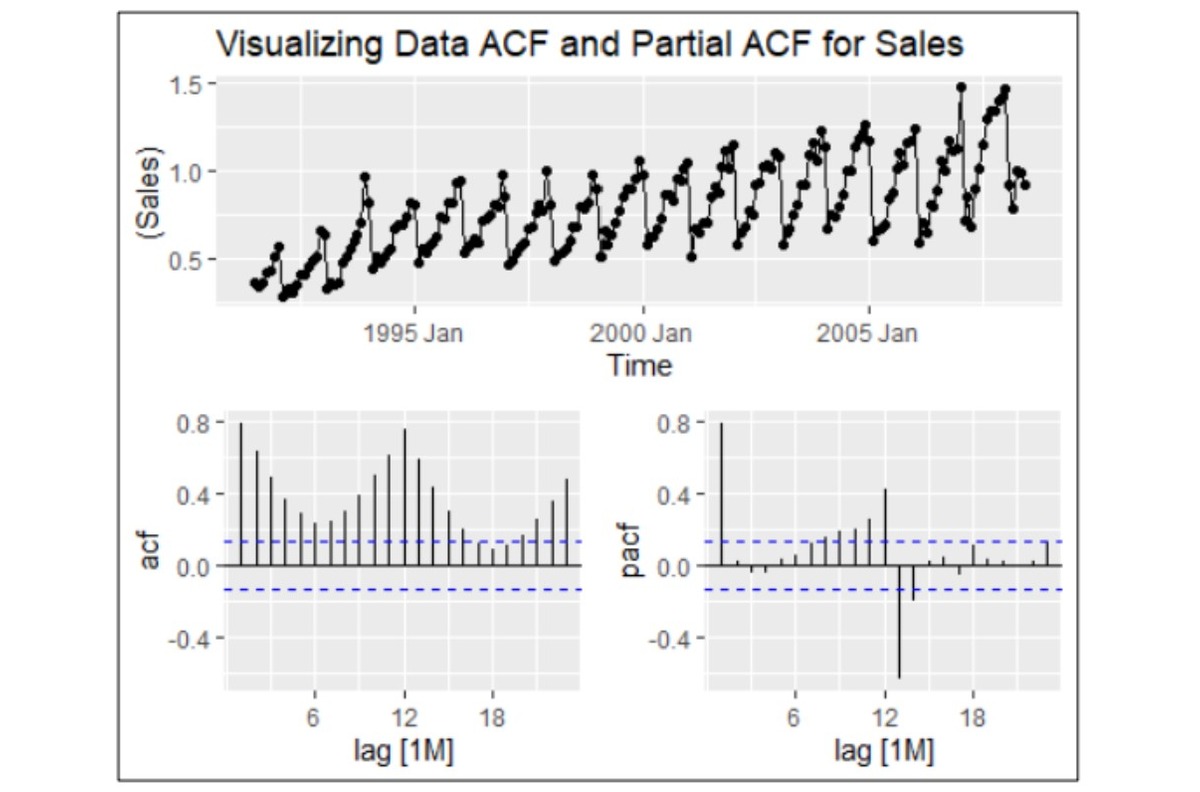
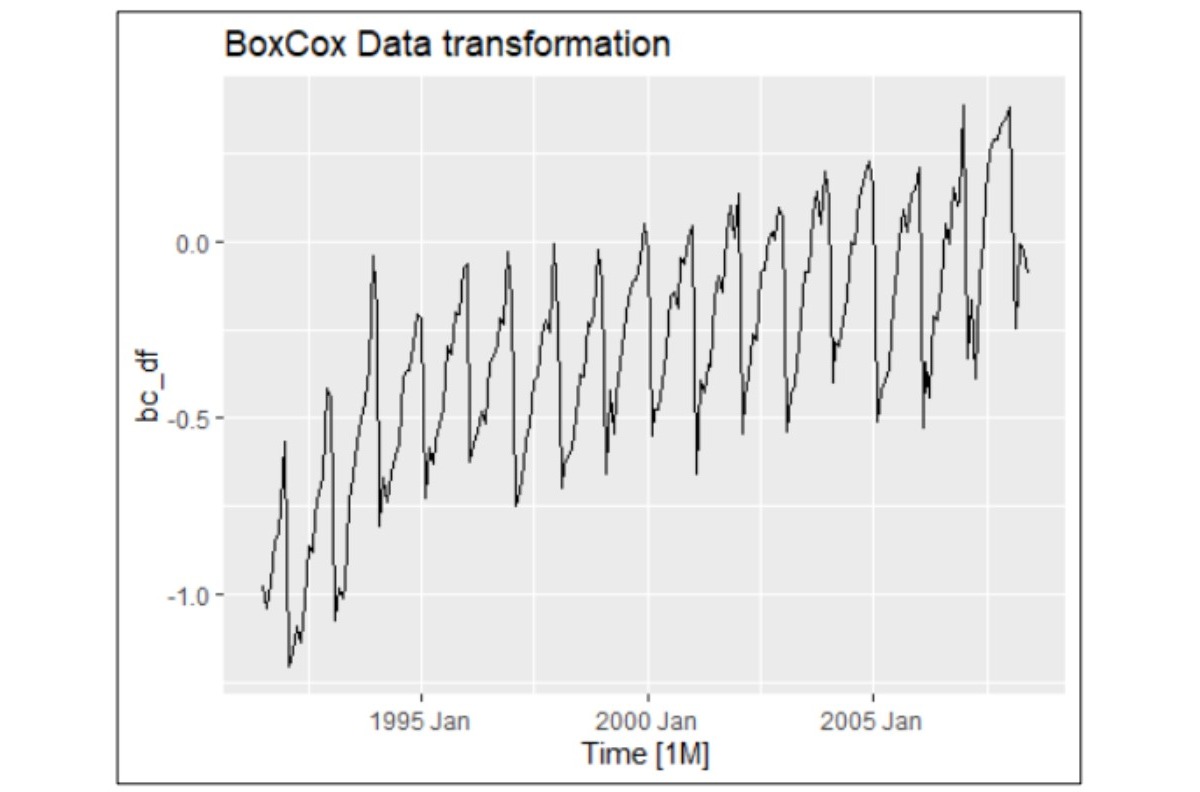
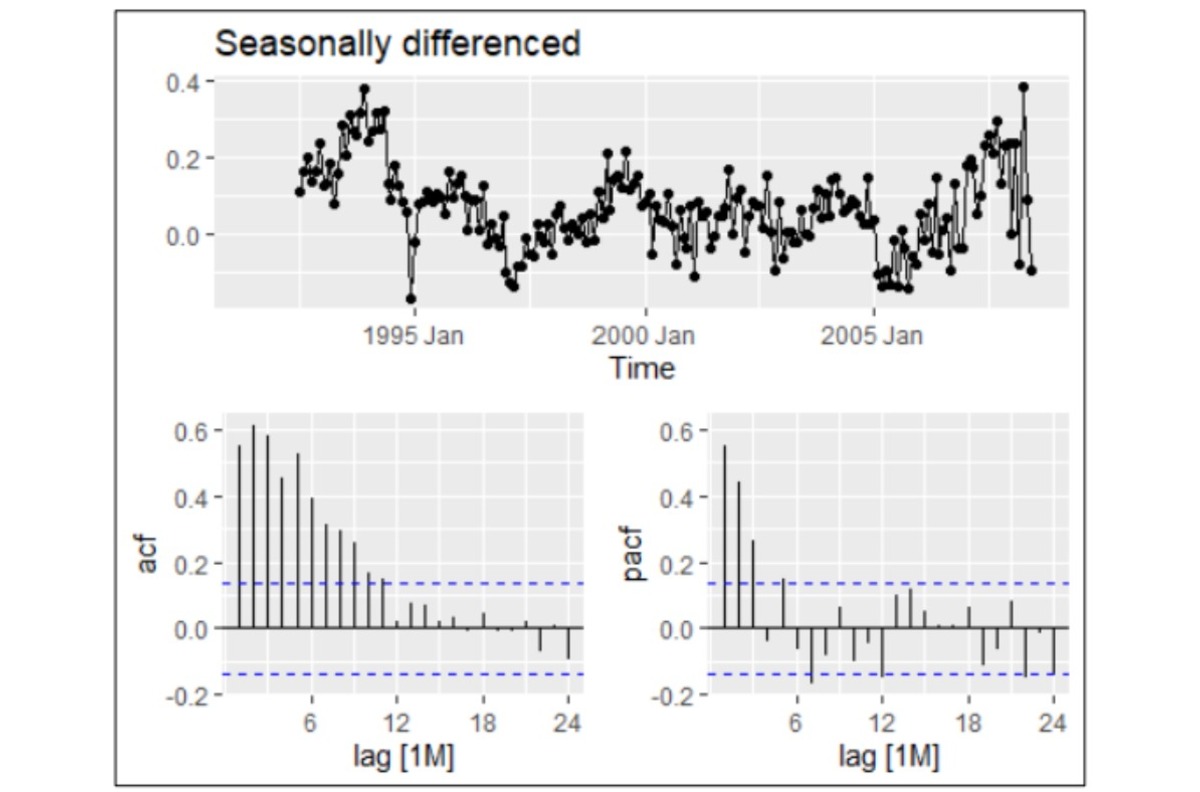
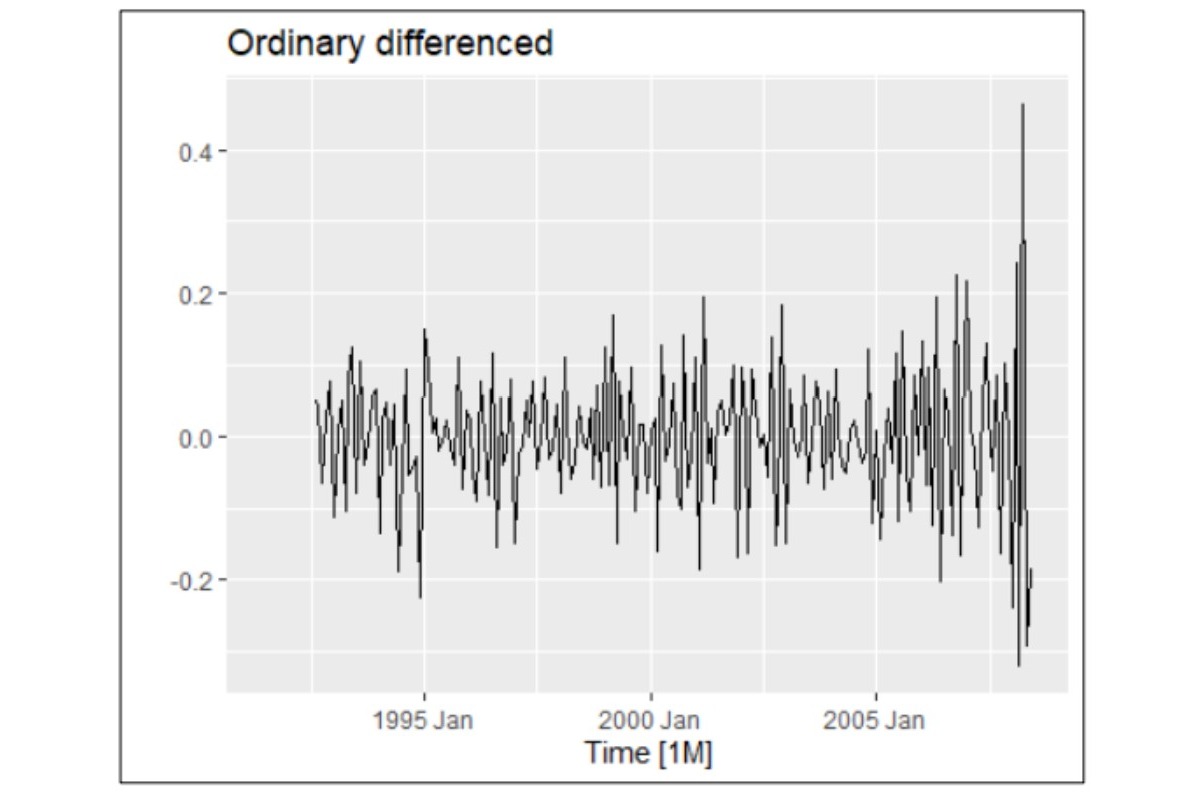
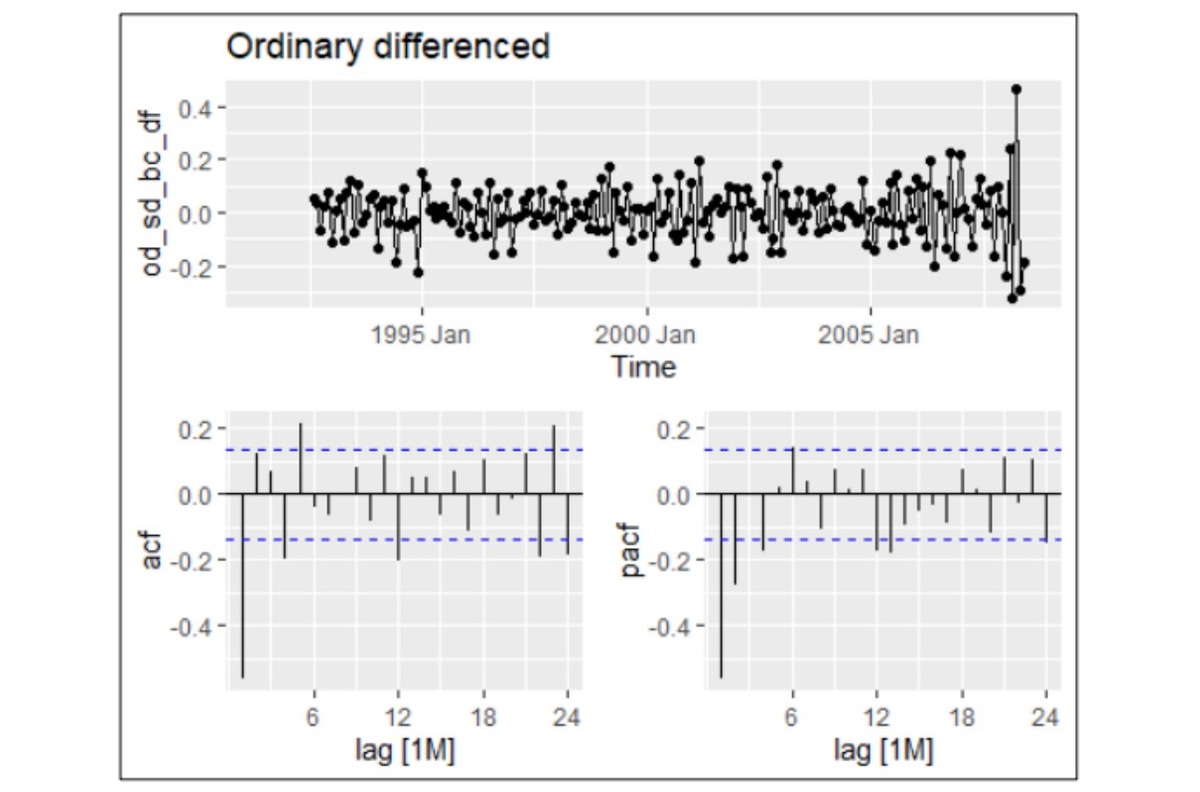
HO3 Drug Sales dataset: This dataset exhibits strong seasonal patterns, proportional sales variations, and a gradual upward trend, indicating non-stationary time series behaviour. These features make it an excellent candidate for testing and comparing forecasting models.

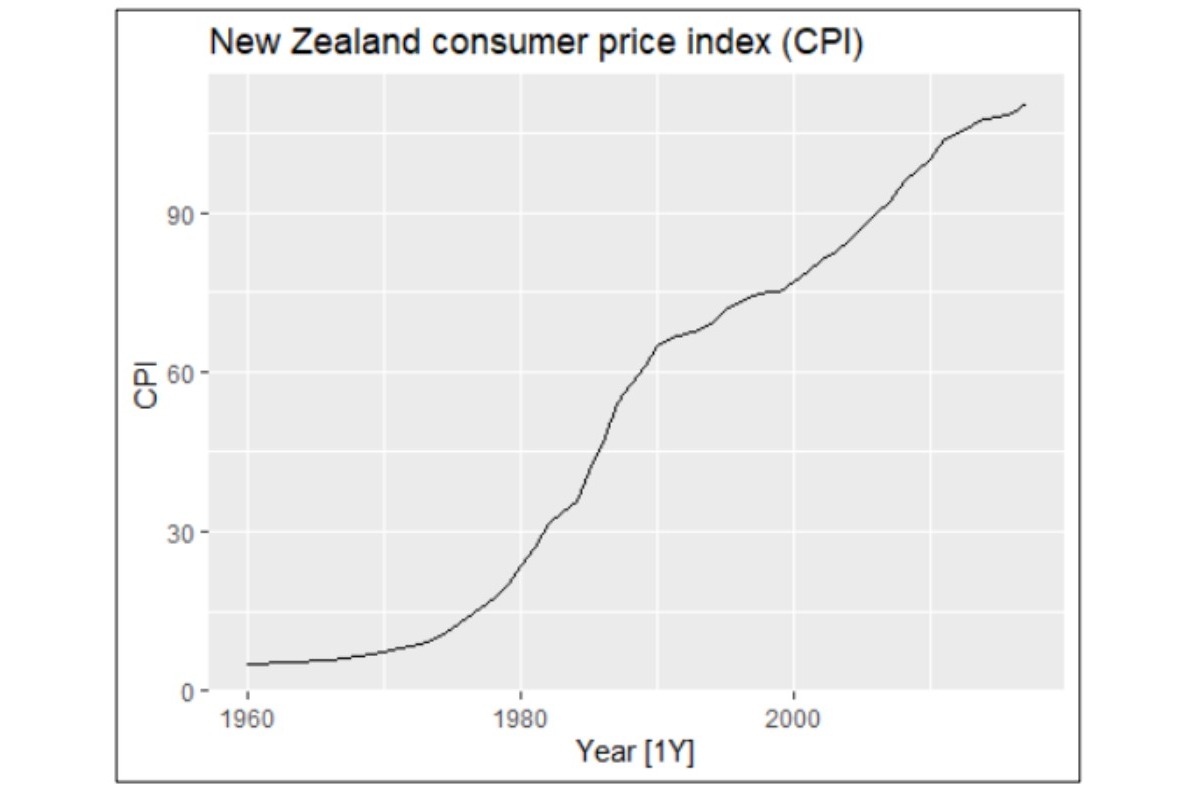
New Zealand economy dataset: This dataset reflects macroeconomic trends, offering insights into economic fluctuations. It was specifically used to evaluate forecasting models for non-seasonal yet trend-driven time series.

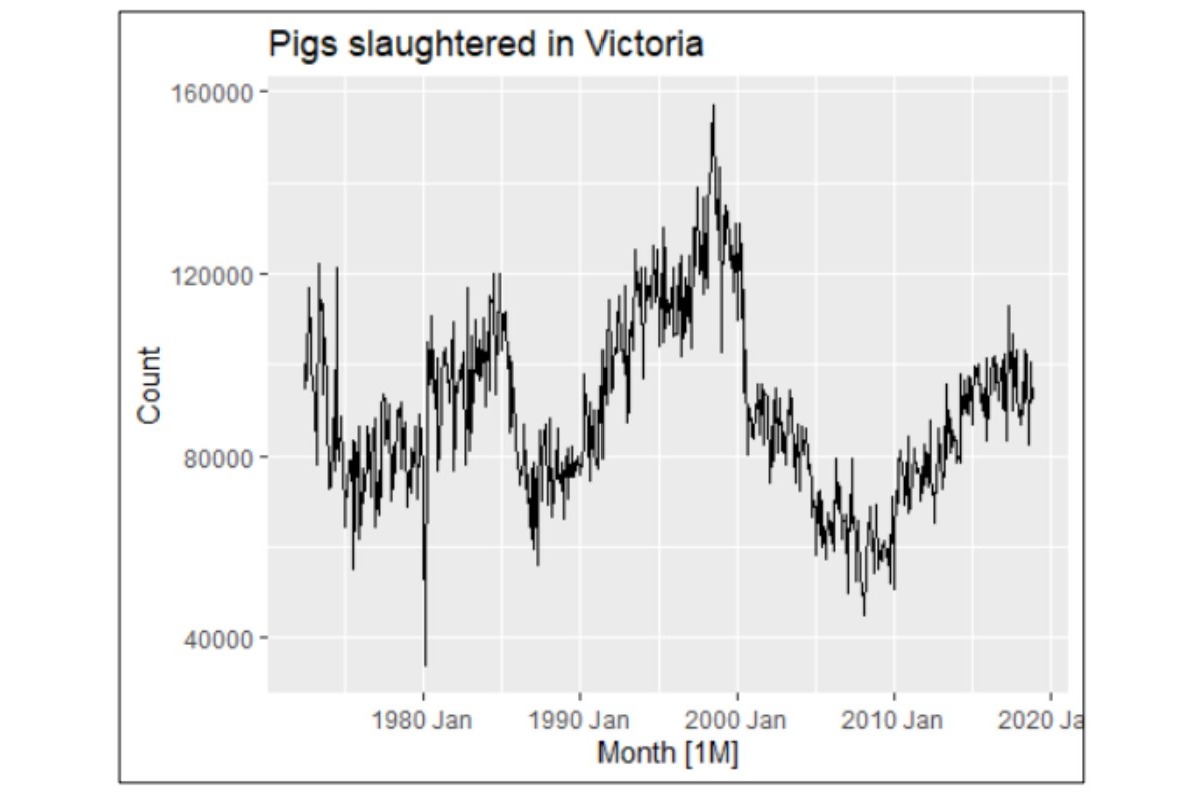
Australia livestock dataset: This dataset captures the number of pigs slaughtered in Victoria over time. It presents partial seasonality alongside fluctuating trends, providing a unique challenge for forecasting models designed to handle mixed patterns.

Objective

The primary aim of this study is to evaluate and compare the performance of ETS and ARIMA models for forecasting time series data. Key objectives include:

Identifying trends, seasonality, and variations within the datasets.
Assessing the accuracy of models like Holt-Winters (ETS) and ARIMA using metrics such as MAE and MSE.
Recommending the most suitable forecasting method based on the datasets' unique characteristics and forecast horizons.

Tools and Techniques Used

Programming Language: R
ETS Models: Holt’s Linear Trend (HLT), Holt’s Damped Trend (HDT), and Holt-Winters (HW) with additive and multiplicative methods.
ARIMA Models: Seasonal and non-seasonal ARIMA configurations, optimised using AICc and validated with residual diagnostics.
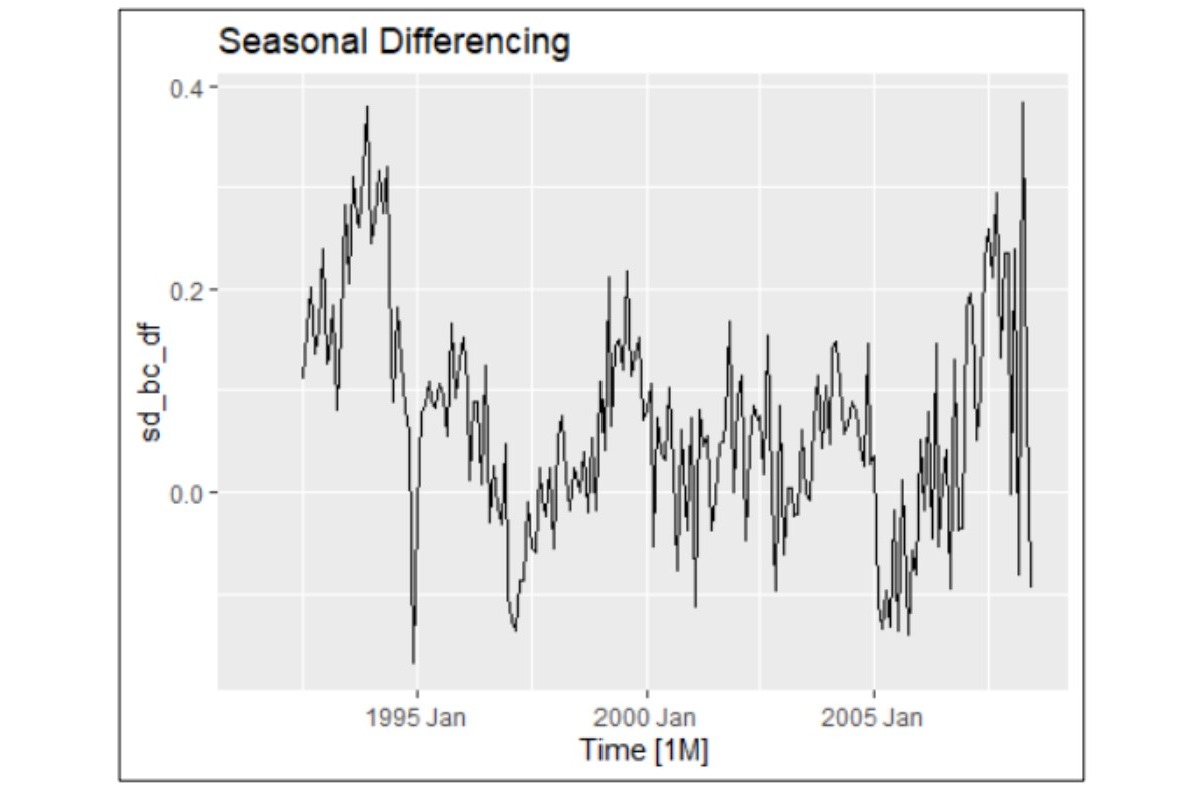
Seasonal Differencing: Applied to stabilise non-stationary series by removing trends and seasonal components.
Accuracy Metrics: MAE, MSE, and residual analysis to evaluate model performance.

Conclusion

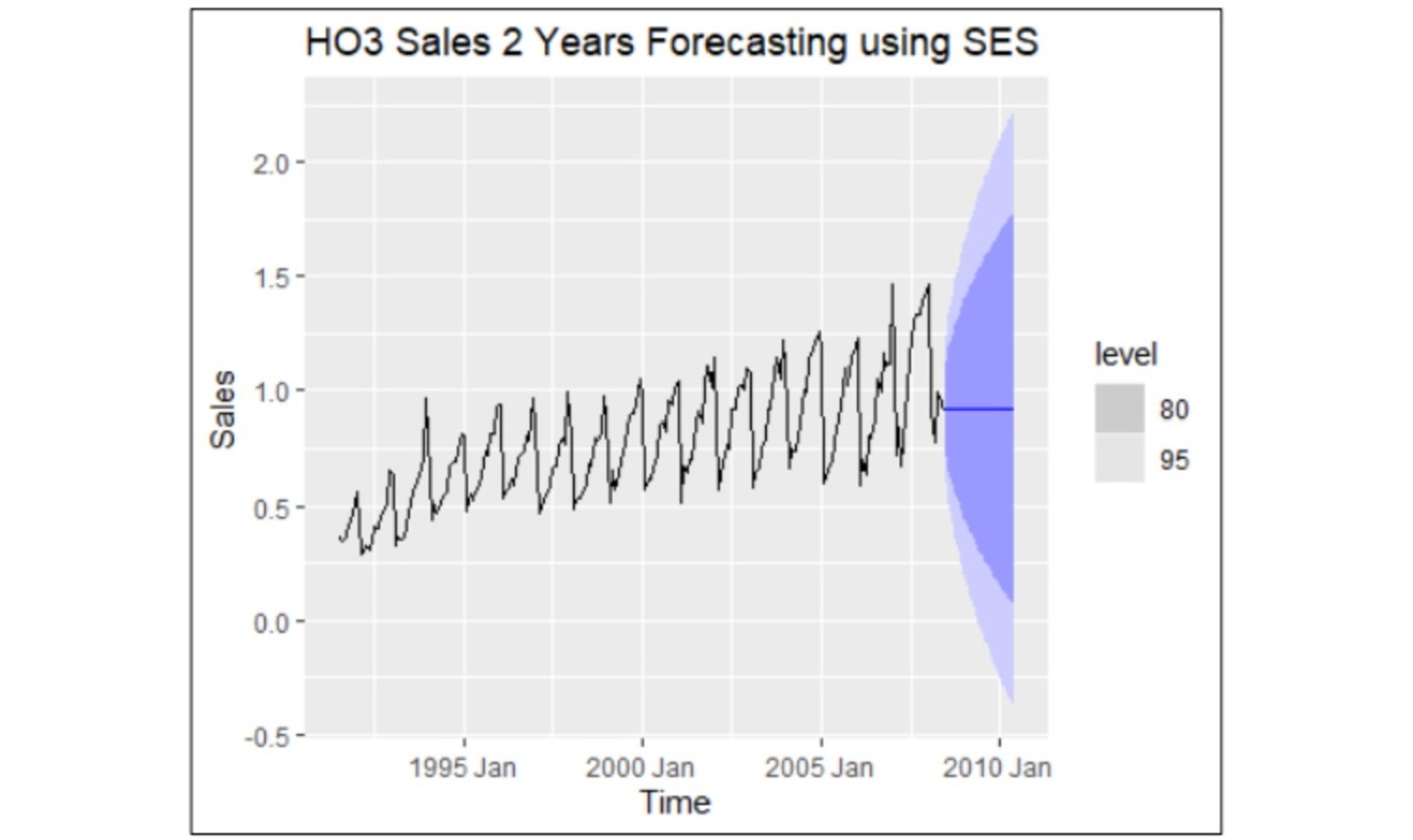
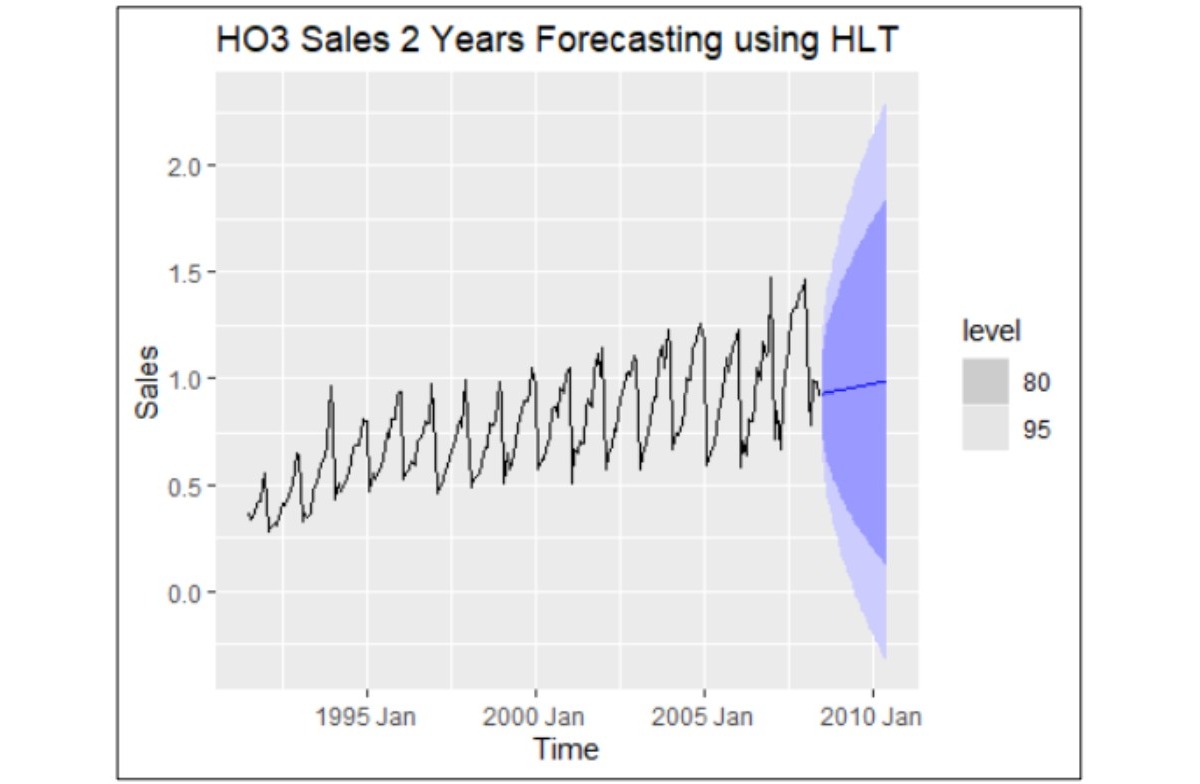
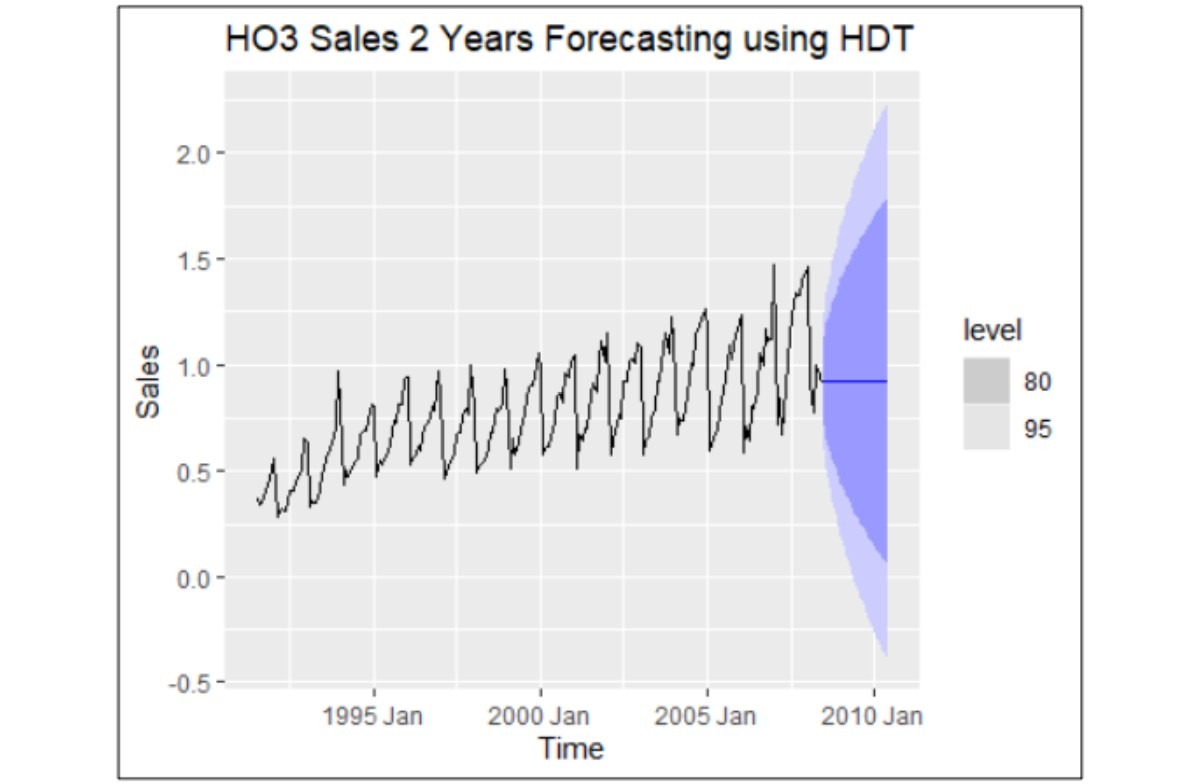
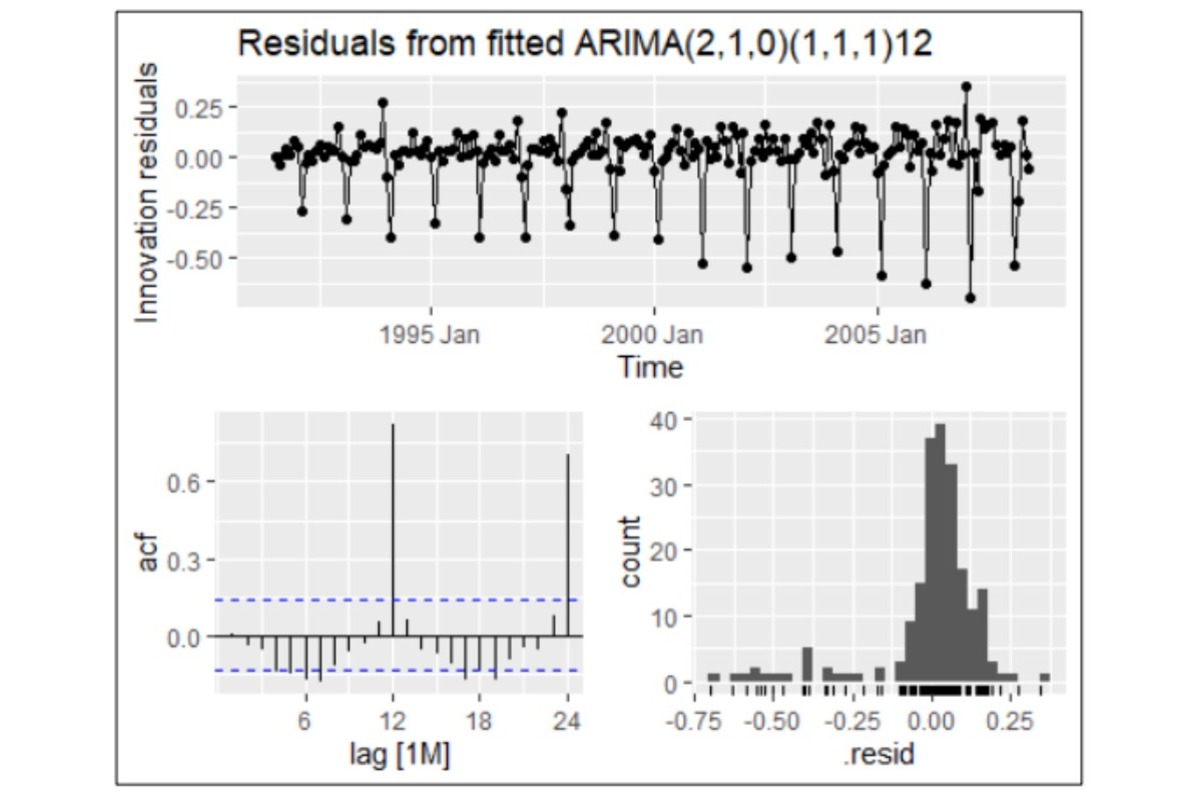
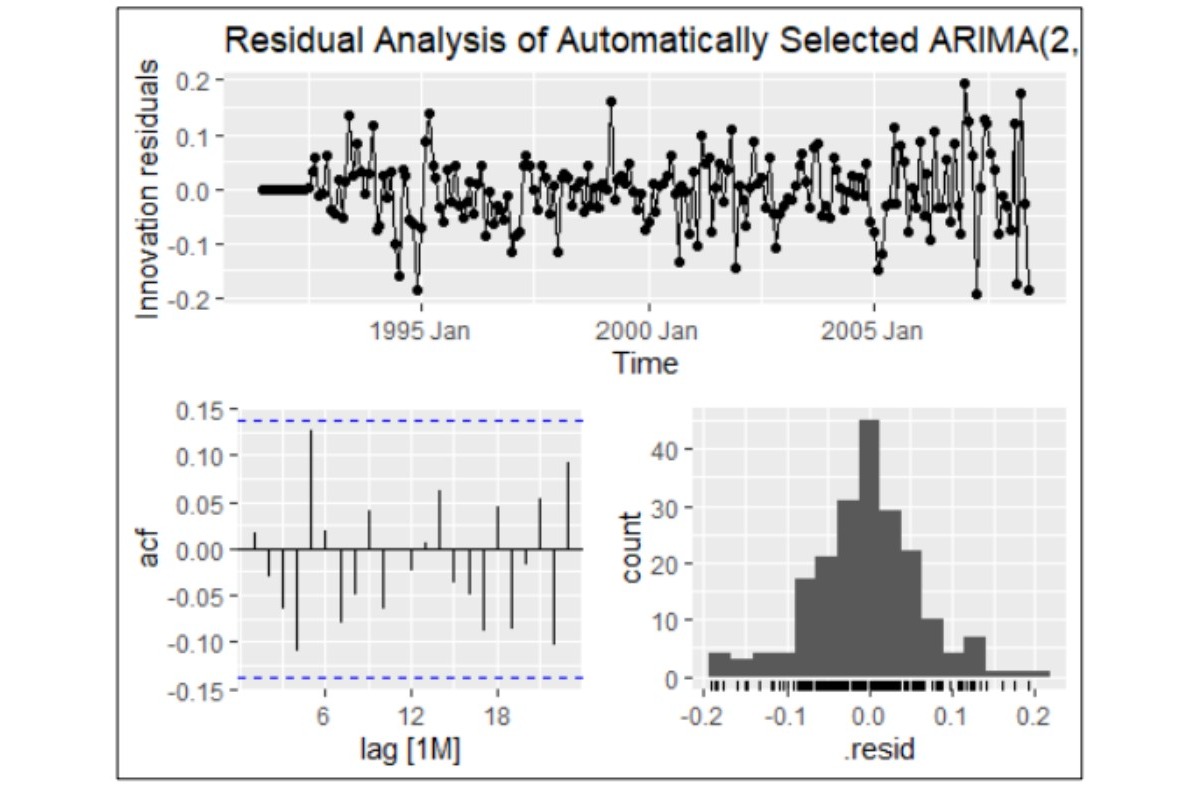
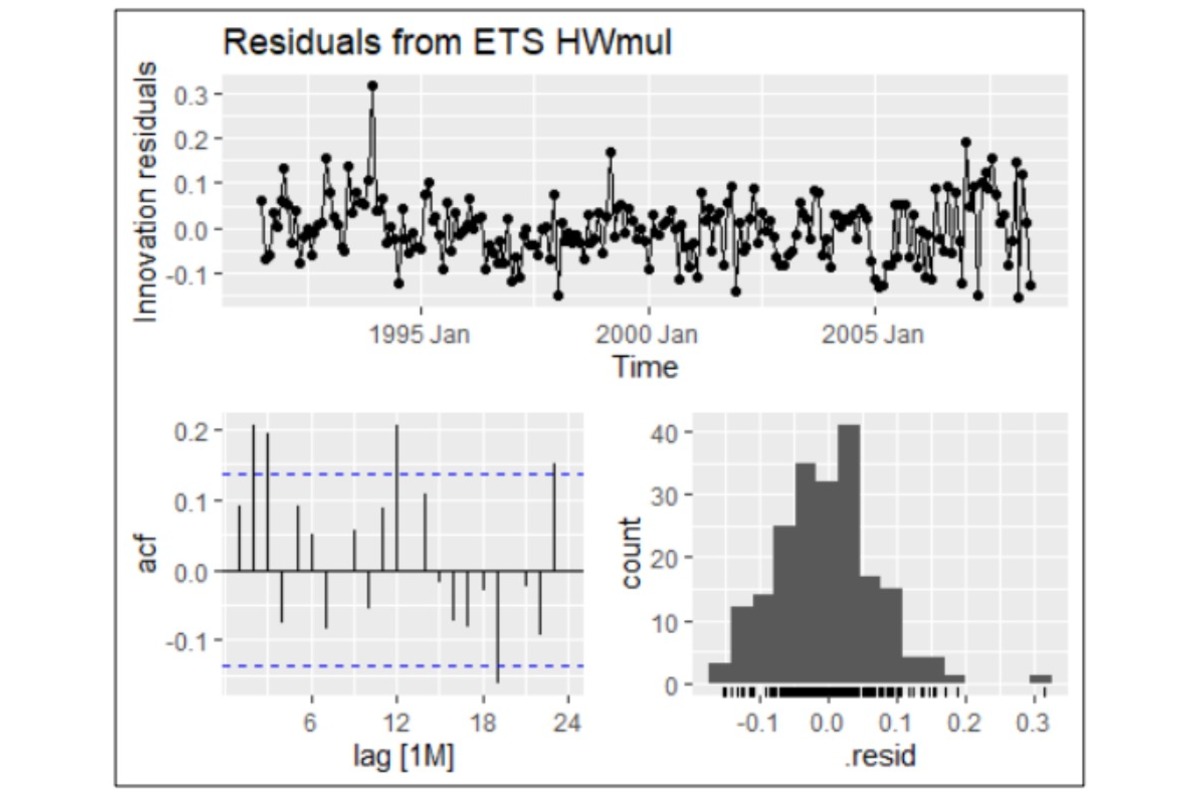
HO3 Drug Sales dataset: The ARIMA model proved superior for forecasting this dataset, exhibiting residuals with characteristics such as white noise, normal distribution, and a mean close to zero. In contrast, the ETS model's residuals deviated from randomness, showing evidence of non-random patterns. This indicates that ARIMA is better suited for capturing the complexities of this dataset.

New Zealand economy dataset: Due to the dataset's linear uptrend and lack of clear seasonality, Holt’s Linear Trend (HLT) was the most appropriate model. The Holt-Winters models, which are designed for seasonality, returned NaN values for accuracy metrics, underscoring the non-seasonal nature of the data.

Australia livestock dataset: This dataset revealed an inconsistent trend, with an upward trajectory from the late 1980s to the late 1990s, followed by a decline towards the 2000s. While seasonality was not immediately apparent, the Holt-Winters additive model (HWad) performed best, demonstrating high accuracy with low error metrics. The absence of warnings or NaN values further suggests a level of seasonality and trend within the dataset.

Ultimately, the choice of a forecasting method depends on the forecast horizon and the dataset's characteristics. ETS models excelled in capturing seasonality and proportional variations, while ARIMA models were more effective for datasets with minimal seasonal patterns. These findings highlight the importance of aligning model selection with the specific features of the time series and the forecasting requirements.

See Complete Project Here